Während mathematische Analyseverfahren mit inkonsistenten Daten zurechtkommen, ist bei Machine Learning große Datensorgfalt gefragt. Beide Methoden funktionieren sehr unterschiedlich und haben verschiedene Anforderungen und Anwendungszwecke. Worauf beim Einstieg in die Verwendung dieser Technologien in Bezug auf die Datengrundlage zu achten ist, lesen Sie hier.
Machine Learning: Garbage in, garbage out
Die Datenanalyse – oder auch „Data Analytics” – ist eine wichtige Säule der Digitalisierung. Ihr Lebenselixier ist nicht die größtmögliche Datenmenge, sondern die Güte der Eingangsdaten. Und genau hier liegt das Problem: Die Praxis zeigt, dass das verwendete Datenmaterial oft fehlerbehaftet oder unvollständig ist. Trotzdem starten viele Unternehmen mit Data Analytics durch. Doch macht das wirklich Sinn? Ja, wenn es sich um mathematische Analyseverfahren handelt. Nein, wenn es um Machine Learning geht.
Machine Learning verzeiht keine Datenprobleme
Alles was unter den Begriff „Machine Learning” fällt, basiert auf der Idee, dass ein System mit bekannten Daten trainiert wird und nach der Trainingsphase bei einer neuen Situation die richtige Antwort liefert. Beispiel: Das System ist in der Lage, eine Katze in einem Bild zu erkennen.
Fehlen Eingangsdaten oder sind sie unvollständig, ist keinerlei Training zielführend. Bezogen auf das obige Beispiel bedeutet das, dass das System vorhandene Katzen übersieht. Es braucht mehr Dateninput, um zu lernen, was eine Katze charakterisiert.
Fehlerhafte Eingangsdaten wirken sich ebenfalls desaströs auf Machine-Learning-Projekte aus: Bleiben fehlerhafte Daten unentdeckt, wird ein System trainiert, welches in Zukunft falsche Ergebnisse liefern wird. Um beim obigen Beispiel zu bleiben: Das System erkennt nicht nur Katzen als solche, sondern identifiziert auch Hunde und Stühle als Katzen. Werden die Ergebnisse ohne Prüfung direkt weiterverarbeitet, zieht sich schlussendlich der Fehler durch viele Stufen des Geschäftsprozesses. Je später der Fehler erkannt wird, desto kostenintensiver fällt seine Beseitigung aus. Ergo: Das Einspeisen fehlerhafter Daten ist bei Machine Learning hoch riskant und muss unbedingt vermieden werden.
Tendenziöse Eingangsdaten haben ebenfalls ihre Tücken: Der Spruch „Traue keiner Statistik, die du nicht selbst gefälscht hast” ist landläufig bekannt. Dahinter steckt nichts anderes, als dass man durch die geschickte Auswahl an Basisdaten das Ergebnis stark beeinflussen kann. Im obigen Beispiel erkennt das System nur weiße Katzen als solche; normale Hauskatzen fallen durch das Raster.
Fazit:
Machine Learning macht ausschließlich mit einer sehr hohen Datenqualität Sinn – alles andere ist reine Zeit- und Geldverschwendung. Bevor man aktiv in das Machine Learning einsteigt, ist es also zwingend notwendig, das Grunddatenmanagement soweit zu optimieren, dass konsistente Daten vorliegen. Die Erfahrung erfolgreicher Machine Learning Projekte zeigt, dass 80 % des Gesamtaufwandes in der Datenvorbereitung liegen.
Mathematische Analyseverfahren haben Nachsicht
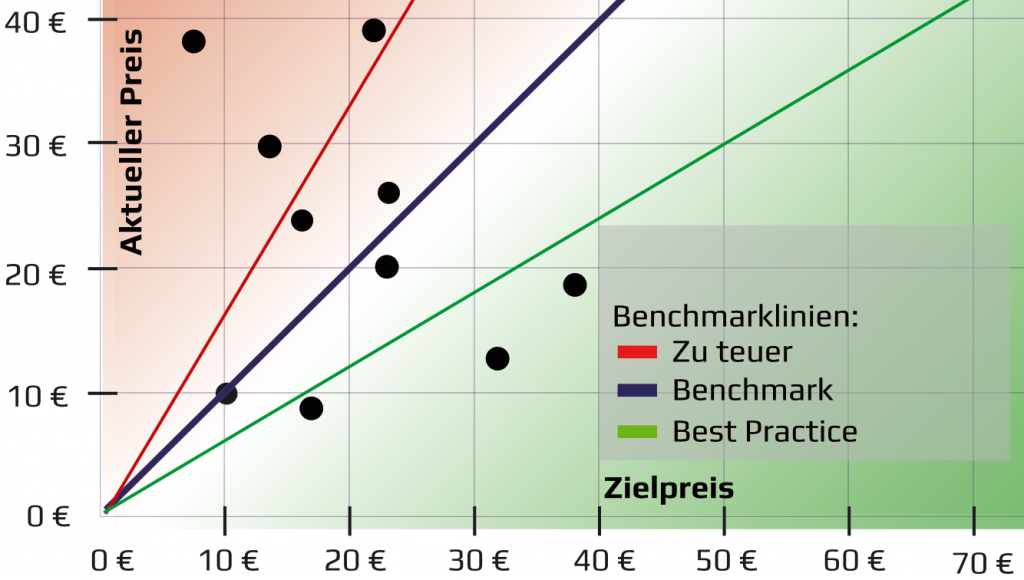
Mathematische Analyseverfahren verfolgen ein anderes Ziel als das Machine Learning: Sie untersuchen Daten nach gewissen Strukturen oder Zusammenhängen/Korrelationen und erlauben damit Prognosen. So kann beispielsweise die Angemessenheit von Einkaufs- und Verkaufspreisen per Regressionsverfahren analysiert werden. Zudem ist es möglich, Preisprognosen für die Zukunft abzugeben („Das Beschaffungsobjekt mit diesen Spezifikationen wird im Einkauf X Euro kosten”).
Generell gilt:
Im Gegensatz zum Machine Learning erheben mathematische Verfahren keinen Anspruch auf Datenkonsistenz, erfordern jedoch ein iteratives Vorgehen mit Verifikation der Analyseergebnisse (s. u. „Fazit”). Die Ergebnisqualität entsteht durch Testen, Bereinigen und Auditieren der genutzten Daten in jeder Phase der Analyse.
Fehlende oder unvollständige Eingangsdaten stellen für mathematische Analyseverfahren aus zwei Gründen kein Problem dar: Einerseits lässt sich die Art der Analyse flexibel am Vorhandensein einzelner Parameter ausrichten. Andererseits kommen die mathematischen Verfahren auch mit erheblich kleineren Datenmengen zu validen Ergebnissen, sodass die lückenhaften Datensätze im Vorfeld einfach aussortiert werden können.
Wirken sich fehlerhafte Eingangsdaten gravierend auf das Analyseergebnis aus, so lassen sie sich einfach als solche entlarven: Das Analyseergebnis wirkt im Rahmen der Verifikation schon auf den ersten Blick falsch.
Tendenziöse Eingangsdaten würden die Ergebnisse der mathematischen Analyse verzerren. Bezieht man in die Preisanalyse beispielsweise ausschließlich die schlechtesten Angebotspreise ein (und lässt die günstigen absichtlich außen vor), erhalt man Preisprognosen, die „zu teuer” sind.
Fazit:
Bei mathematischen Analyseverfahren ist die Einstiegshürde in die Welt der Data Analytics hinsichtlich der Datenbereinigung viel geringer als beim Machine Learning. Um bei dem Beispiel der Preisanalyse zu bleiben: Mittels der mathematischen Analysemethode Non-linear Performance Pricing findet ein Einkäufer heraus, dass zwei seiner Beschaffungsobjekte aufgrund ihrer Eigenschaften eigentlich gleich viel kosten müssten – in der Realität weichen die Einkaufspreise jedoch stark voneinander ab. Jetzt geht es an die Verifikation der Ergebnisse. Der Einkäufer prüft, ob die Teile wirklich die gleichen Eigenschaften aufweisen und die Eingangsdaten dieser beiden Teile fehlerfrei sind (Beispiel: Sind wirklich beide Teile mit Gold beschichtet? Nutzen beide Teile die gleiche Gewichtseinheit? etc.). Stößt er hier auf Fehler, muss die Analyse nach erfolgter Datenkorrektur wiederholt werden. Ist kein Fehler zu finden, ist er auf einen „Hotspot” gestoßen und kann die Ergebnisse der Analyse verwenden. Tendenziöse Eingangsdaten sind jedoch auch bei der mathematischen Datenanalyse in jedem Fall zu vermeiden.
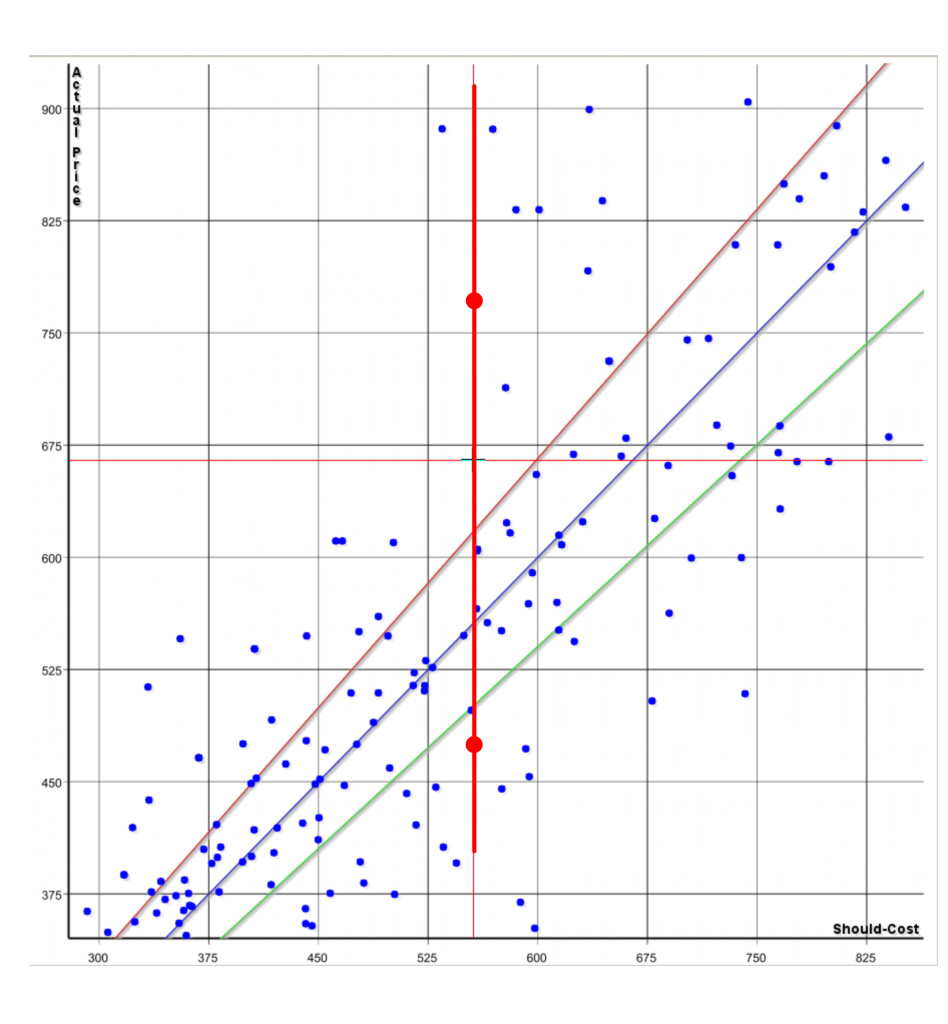
Wann sind Daten eigentlich „perfekt”?
Die „Perfektion” ergibt sich stets im Kontext des Ziels und der jeweiligen Analysemethode. Daten, die für Anwendung A funktionieren, müssen nicht zwangsläufig für Anwendung B geeignet sein. Nur, wenn die „innere Struktur” der Daten der jeweiligen Anforderung entspricht, liefern die Verfahren auch valide und nutzbare Ergebnisse.






